Comprendre les parcours d'un arbre binaire
Maîtriser certaines structures de données, notamment l’arbre binaire, est crucial pour tout développeur. Un arbre binaire est une structure de données composée de nœuds, chacun stockant des données et des pointeurs vers d'autres nœuds. Chaque nœud d'un arbre binaire pointe vers un maximum de deux nœuds, appelés les enfants gauche et droit.
Nous allons explorer en détail ce qu'est un arbre binaire, ses composants, ainsi que les méthodes les plus courantes pour parcourir cette structure de manière efficace. Nous illustrerons également ces concepts par des cas d'utilisation concrets pour vous aider à comprendre pourquoi ces connaissances sont cruciales dans un environnement de développement logiciel.
Les Composants d'un Arbre Binaire
Un arbre binaire se compose de plusieurs éléments clés :
- Le nœud racine : Le nœud au sommet de l'arbre, à partir duquel tous les autres nœuds sont accessibles.
- Les nœuds internes : Les nœuds qui ont au moins un enfant.
- Les feuilles : Les nœuds sans enfants, situés en bas de l'arbre.
La nature récursive de l'arbre binaire signifie que chaque nœud peut être vu comme la racine d'un sous-arbre, permettant ainsi de traiter chaque sous-arbre comme un nouvel arbre. Cette propriété rend les parcours récursifs de l'arbre non seulement possibles, mais aussi élégants et efficaces.
Pour parcourir un arbre binaire, deux approches principales sont couramment utilisées : la recherche en profondeur (DFS) et la recherche en largeur (BFS). Chacune de ces méthodes offre une manière unique d’explorer les nœuds de l’arbre, avec des applications spécifiques en fonction des besoins du problème à résoudre. Le DFS explore l’arbre en profondeur, descendant aussi loin que possible avant de revenir en arrière, tandis que le BFS examine les nœuds niveau par niveau, garantissant que tous les nœuds d’un niveau sont explorés avant de passer au suivant.
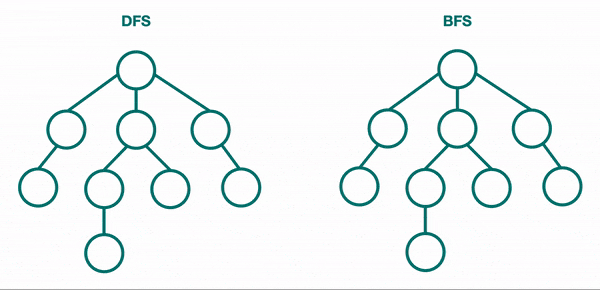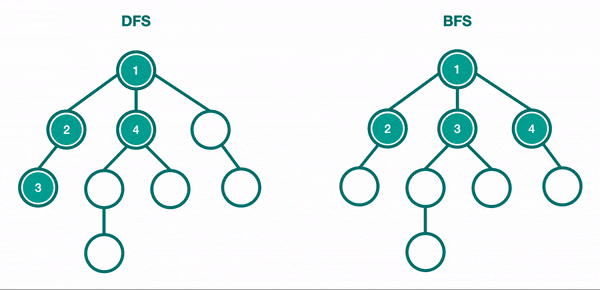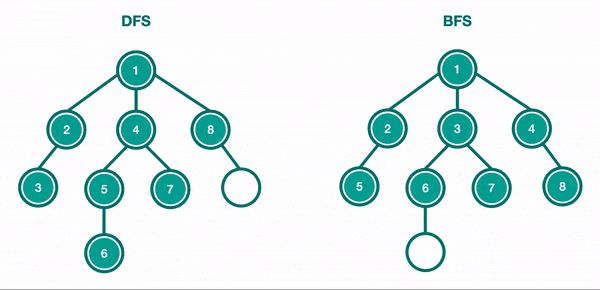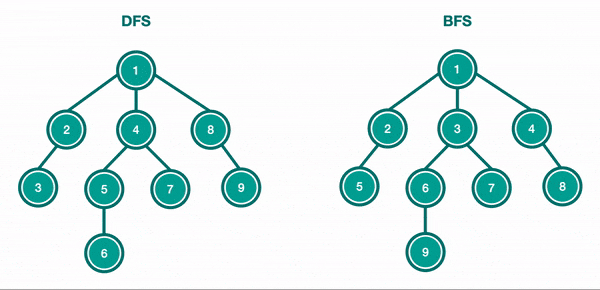
Les Méthodes de Parcours en Profondeur (DFS)
Le Depth-First Search (DFS) est une méthode de parcours qui commence à la racine et explore autant que possible un chemin avant de revenir en arrière. Il existe trois types principaux de parcours DFS, chacun ayant des applications spécifiques :
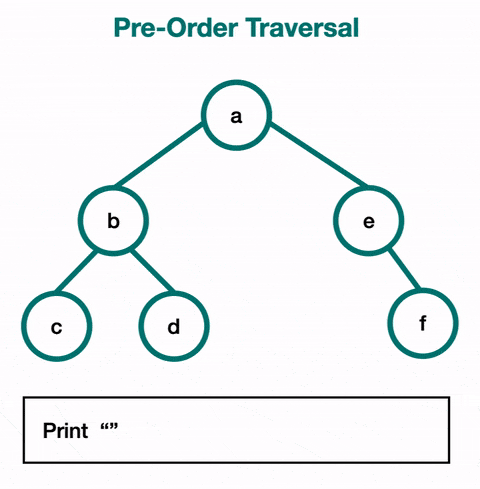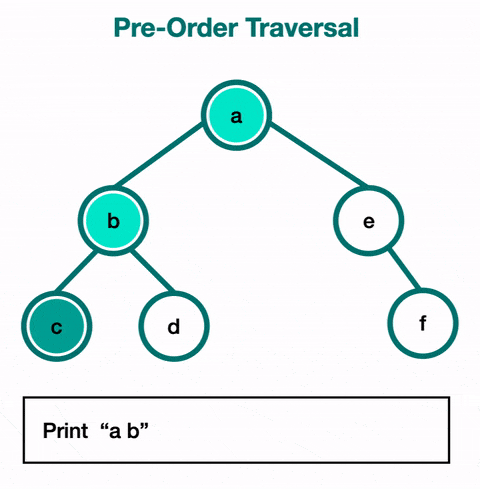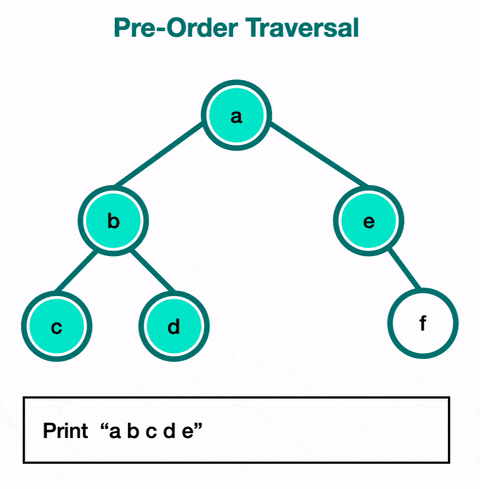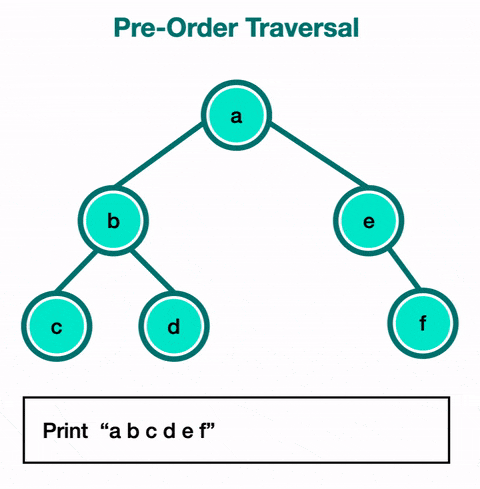
Le parcours en pré-ordre (Preorder Traversal) :
- Dans ce parcours, on visite d'abord un nœud, puis ses enfants.
- Exemple :
print(data)→func(node.left)→func(node.right). - Cas d'utilisation : Ce type de parcours est souvent utilisé pour dupliquer un arbre. En visitant chaque nœud avant ses enfants, on peut créer une copie exacte de la structure d'origine.
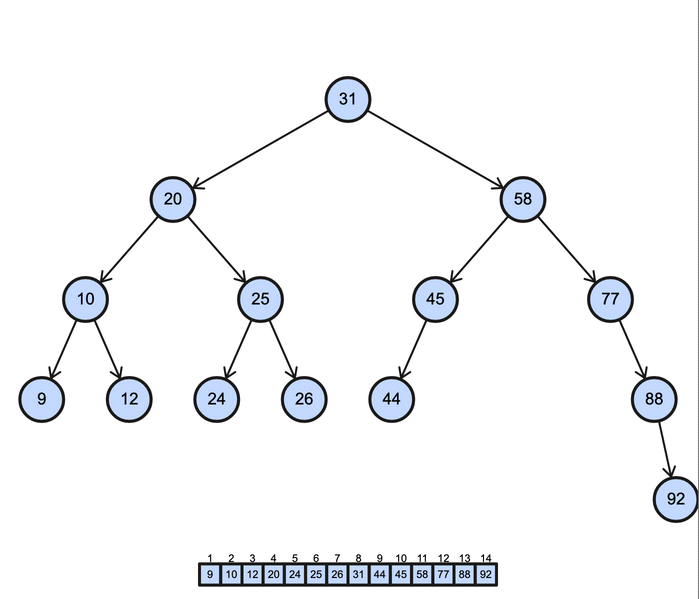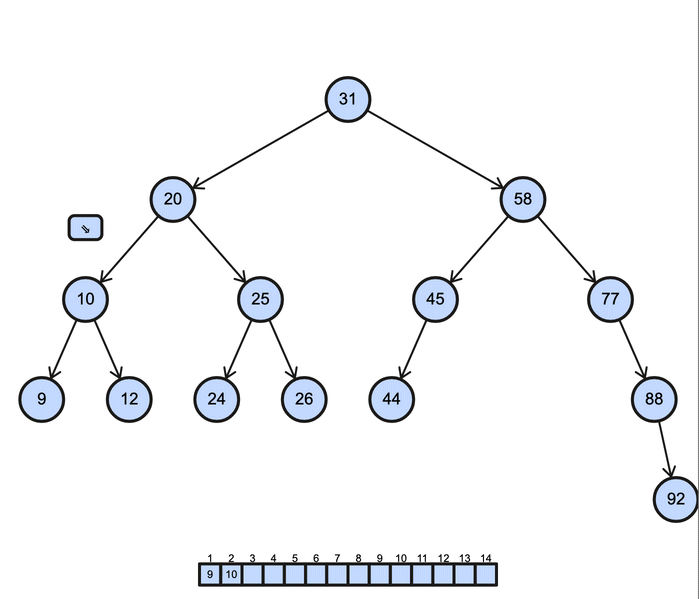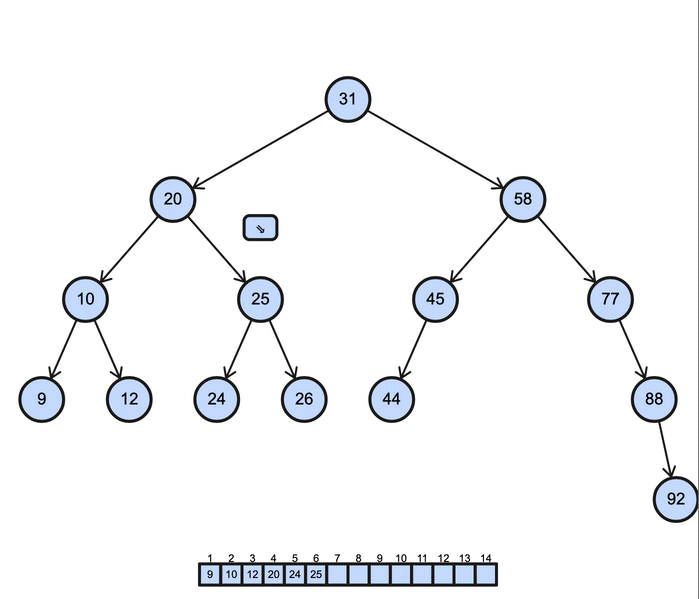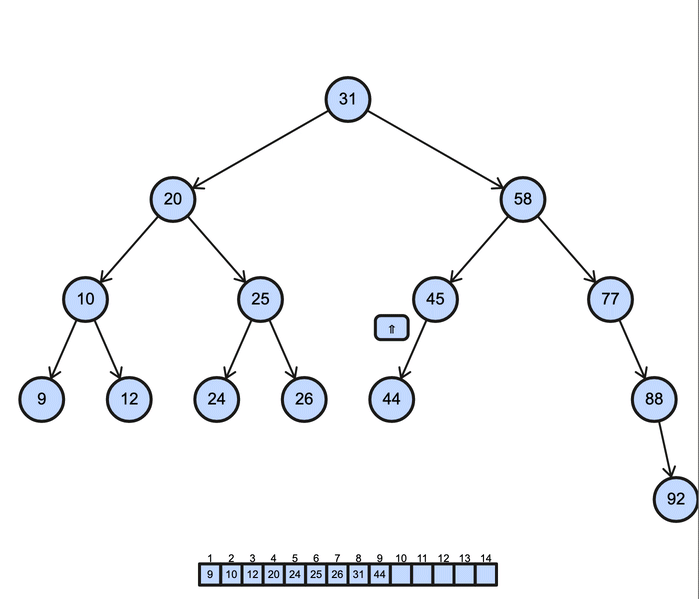
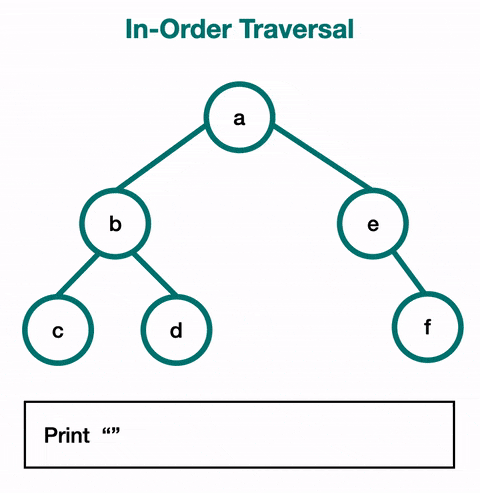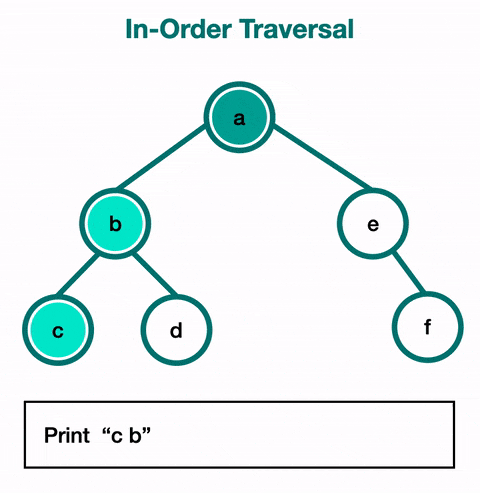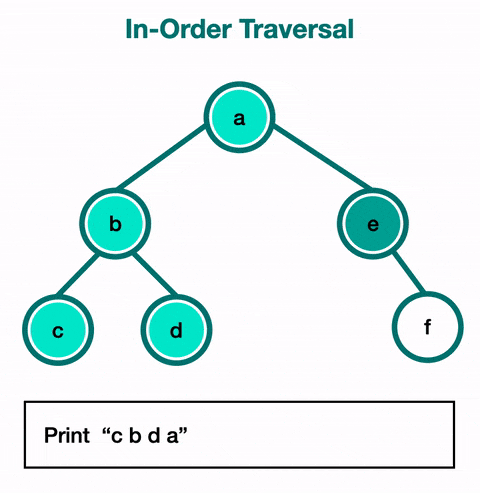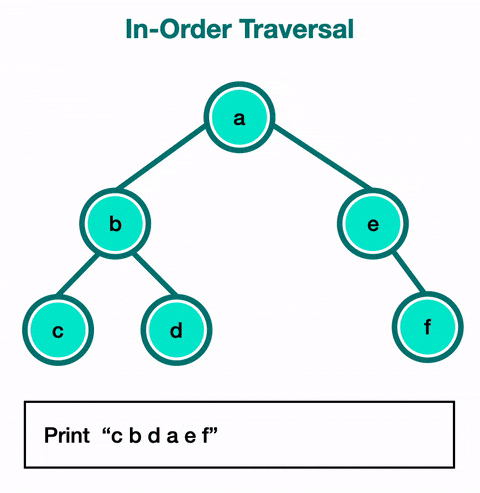
Le parcours en ordre (Inorder Traversal) :
- On visite d'abord le sous-arbre gauche, puis le nœud, et enfin le sous-arbre droit.
- Exemple :
func(node.left)→print(data)→func(node.right). - Cas d'utilisation : Utilisé principalement pour obtenir un ordre croissant des nœuds dans un arbre binaire de recherche (Binary Search Tree - BST), ce parcours est fondamental pour les opérations telles que l'extraction de données triées.
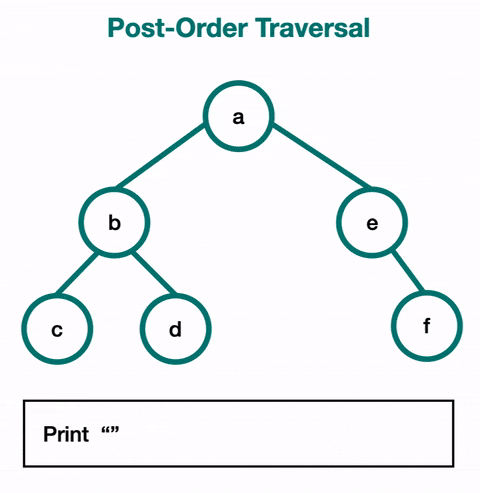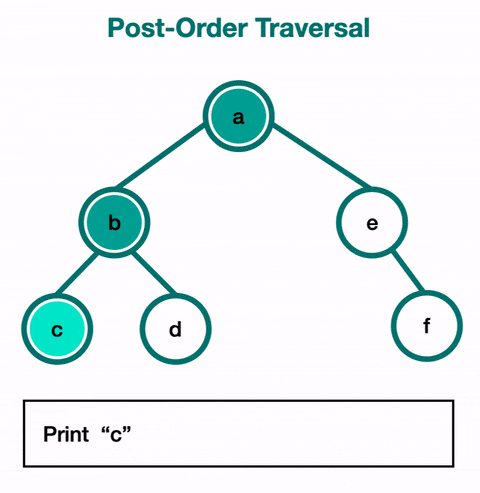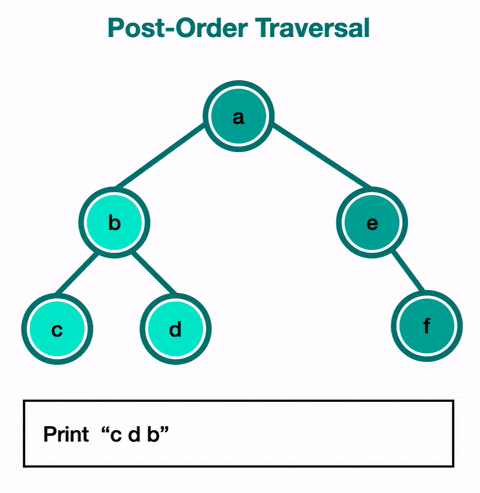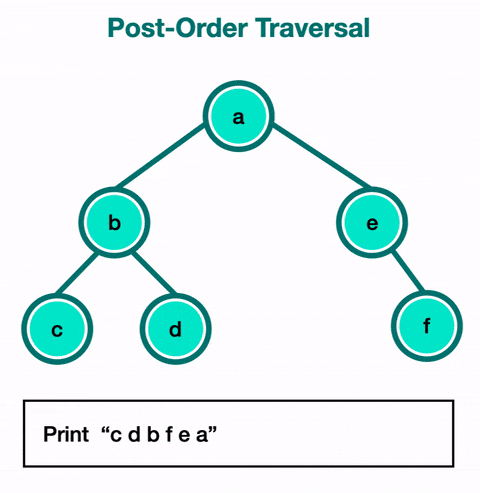
Le parcours en post-ordre (Postorder Traversal) :
- On visite d'abord les enfants, puis le nœud.
- Exemple :
func(node.left)→func(node.right)→print(data). - Cas d'utilisation : Ce parcours est utile pour supprimer un arbre ou pour libérer la mémoire associée à chaque nœud. En visitant les enfants avant le nœud, on s'assure que tous les nœuds fils sont traités avant leur parent.
Le Parcours en Largeur (BFS)
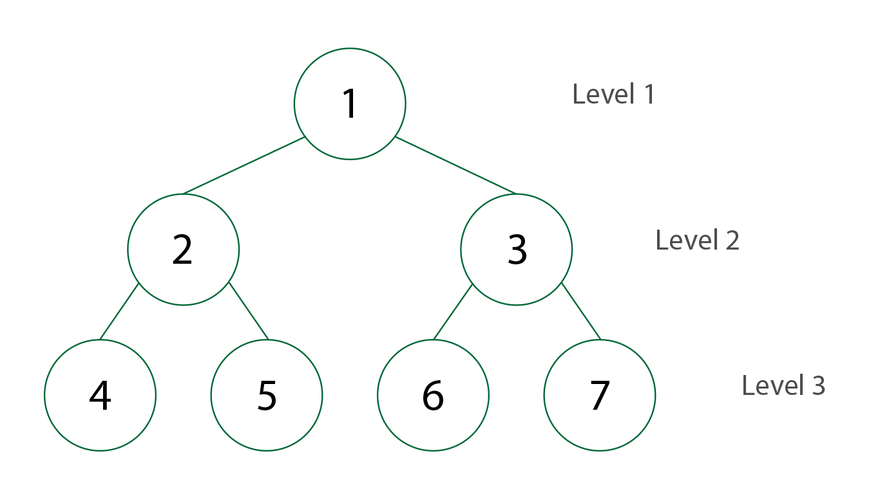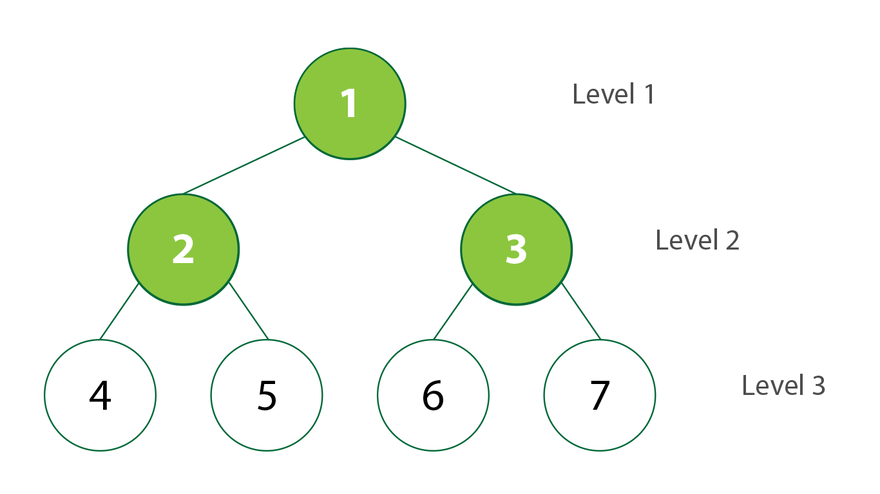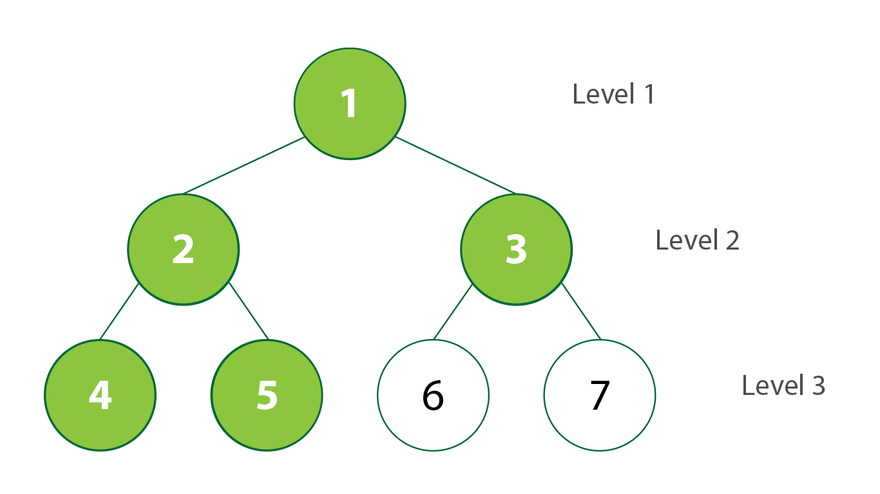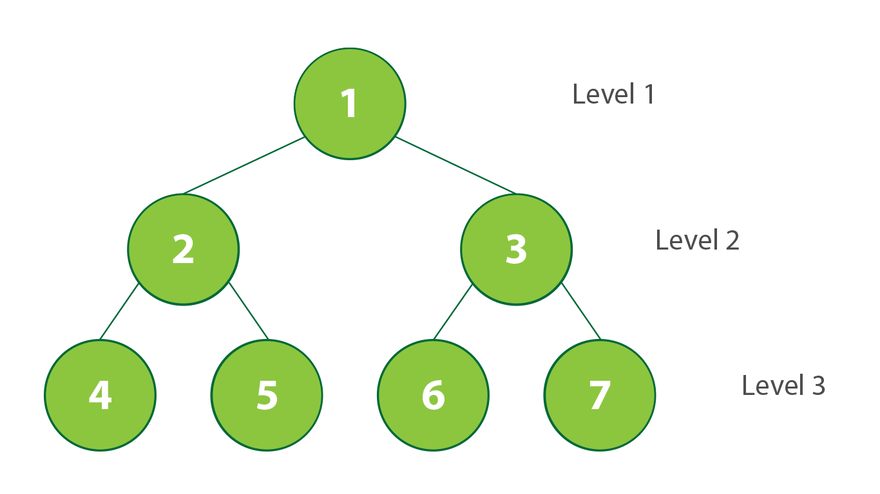
En alternative au DFS, le Breadth-First Search (BFS) explore un arbre niveau par niveau, en commençant par la racine et en parcourant tous les nœuds à une certaine profondeur avant de passer au niveau suivant. Ce parcours utilise généralement une file d'attente (queue) en raison de la nature FIFO (First-In, First-Out) de la structure.
- Cas d'utilisation : Le BFS est particulièrement utile pour trouver le chemin le plus court dans un graphe ou un arbre, ou pour explorer tous les nœuds à un certain niveau avant de descendre plus bas dans la structure.
Conclusion
Maîtriser les parcours d'un arbre binaire est indispensable pour tout développeur sérieux, surtout en vue d'un entretien technique. Les parcours DFS et BFS offrent des approches complémentaires pour explorer des arbres binaires, chacune ayant des applications spécifiques et des avantages distincts. En comprenant ces concepts et en sachant quand les utiliser, vous serez mieux préparé à résoudre des problèmes complexes en programmation et à réussir vos entretiens.
TakkJokk




